High Performance Computing
Simulation of fluid flows can be prohibitively expensive, especially for high Reynolds number (turbulent) flows where vortices have dramatically different sizes. To resolve these vortices, especially those with very small sizes, the computational grid has to be very fine, resulting in excessive computational cost. Meanwhile, finer grid requires smaller time step size, which further increases the overall computational cost. For example, direct numerical simulation (DNS) of a turbulent flow at a moderate Reynolds number using a single CPU core can take hundreds of years to complete.
High performance computing (HPC) on massively parallel computer clusters is one of the most effective ways to address the aforementioned challenge. The figure below shows a schematic of the structure of a typical HPC cluster. The compute nodes are interconnected to each other (e.g., using Ethernet or InfiniBand switches) to allow mutual communications in a local network. The master node (or login node) is connected to both this local network and the outer world to allow users to remotely manage jobs on the compute nodes. Each node usually has its own local storage, memories, and synchronized operating system. The overall cluster can also have external shared file systems with very large capacity (Petabytes, for example) for data storage.

My experience with HPC started in 2009 when I was a Ph.D. student at University of Notre Dame doing research on compressible turbulent flow simulation using a solver called "CDP" developed at Stanford University's Center for Turbulence Research. I was initially running test cases on a cluster with 200+ CPU cores, and then moved to much larger supercomputers (with hundreds of thousands of cores) located at national computing centers. The pictures below are some of the supercomputers that I have used in the past years. In addition to being a user, I also rebuilt and managed a small cluster with 240 cores at the Computational Aero and Hydrodynamics Laboratory in the George Washington University (see the CAHL Cluster WikiPage for more information).






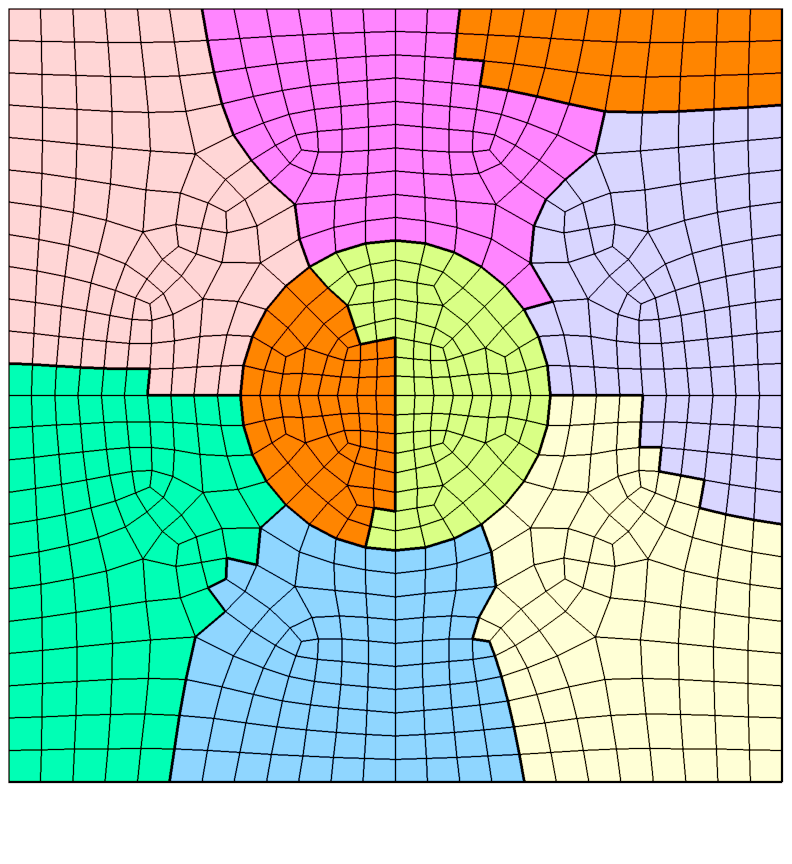
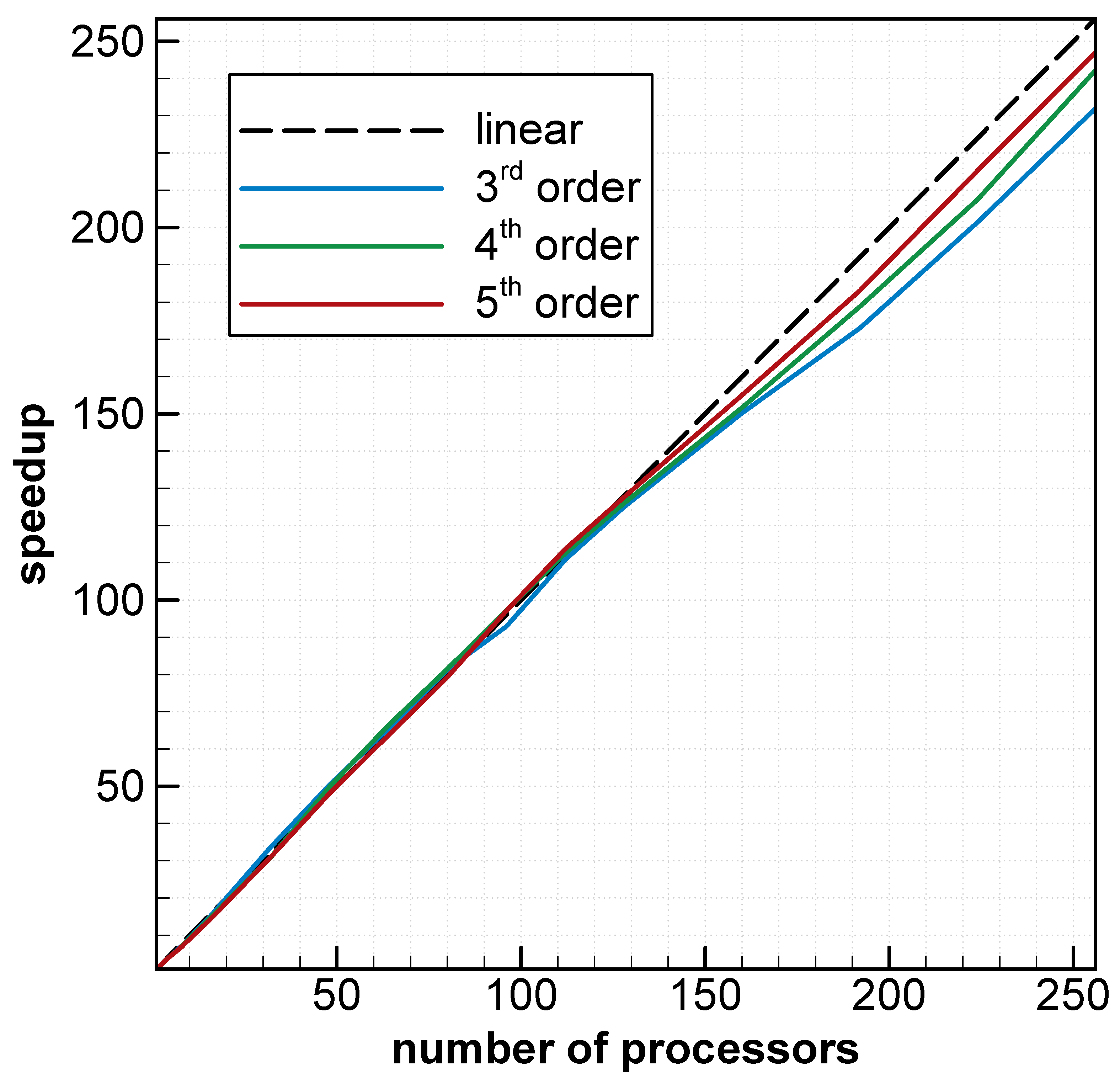
My experience on parallel program development also dates back to 2009. At that time, I developed multiple parallel programs (e.g., for interpolation and integration on unstructured grids) using the Message Passing Interface (MPI) standard. In 2012, I started developing my own high-order accurate and massively parallel flow solvers that work on both stationary and dynamic unstructured meshes. The fundamental idea for parallelization is simple: decompose a mesh into small partitions, then distribute each partition to a processor for computation, and inter-processor communication (data exchange) ensures unique and correct solutions. For example, the figure on the left shows the partitions of a simple mesh, where each color represents a partition. The figure on the right shows the parallel efficiency of one of my solvers on a mesh with several thousands of elements. It is seen that the solver approaches the ideal (linear) speedup as the scheme order increases. The development of a good parallel program requires not only in-depth understanding of the algorithm and the design philosophy, but also knowledge of the hardware.