Wall Modeling

Large eddy simulation (LES) for turbulent flows is already less expensive than direct numerical simulation (DNS). However, it is still very expensive for wall bounded flows, where extremely fine grid is required to resolve the very thin boundary layer so that the wall stress and wall heat flux can be predicted correctly. To further reduce the computational cost, we can model the wall effects instead of resolving the boundary layer. This process is called wall modeling.

Many wall models have been proposed over the past decades. For example, the following equilibrium wall model (Kawai and Larsson, 2012) with our modification to take pressure effects into account, $$ \begin{aligned} \frac{d}{dy}\Big[(\mu+\mu_t)\frac{du}{dy}\Big] &= \frac{\partial p}{\partial x},\\[1em] \frac{d}{dy}\Big[(\mu+\mu_t)u\frac{du}{dy} + c_p (\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t})\frac{dT}{dy}\Big] &= 0, \end{aligned} $$ where $y$ is the wall normal direction, $x$ is the wall tangential direction, $\mu$ is the molecular viscosity, $Pr=0.7$ is the Prandtl number, and $Pr_t=0.9$ is the turbulent Prandtl number. The turbulent eddy viscosity $\mu_t$ is taken from a mixing length model $$ \mu_t = \kappa\mu y^+[1-\exp(-\frac{y^+}{A})]^2, $$ where $\kappa=0.41$, $A=17$, $y^+=y u_\tau/\nu$ is the distance from the wall in wall units, $u_\tau=\sqrt{\tau_w/\rho}$ is the friction velocity, and $\tau_w=\mu du/dy$ is the wall shear stress.

The wall model equations are solved on an imbedded Cartesian grid in the near wall region of an LES domain (as illustrated in the figure below). To make the equations well-posed, two boundary conditions are needed: at the top boundary, LES solutions of tangential velocity, temperature and density are interpolated onto the wall model grid as Dirichlet boundary condition; the bottom boundary is treated as either no-slip adiabatic or isothermal wall.

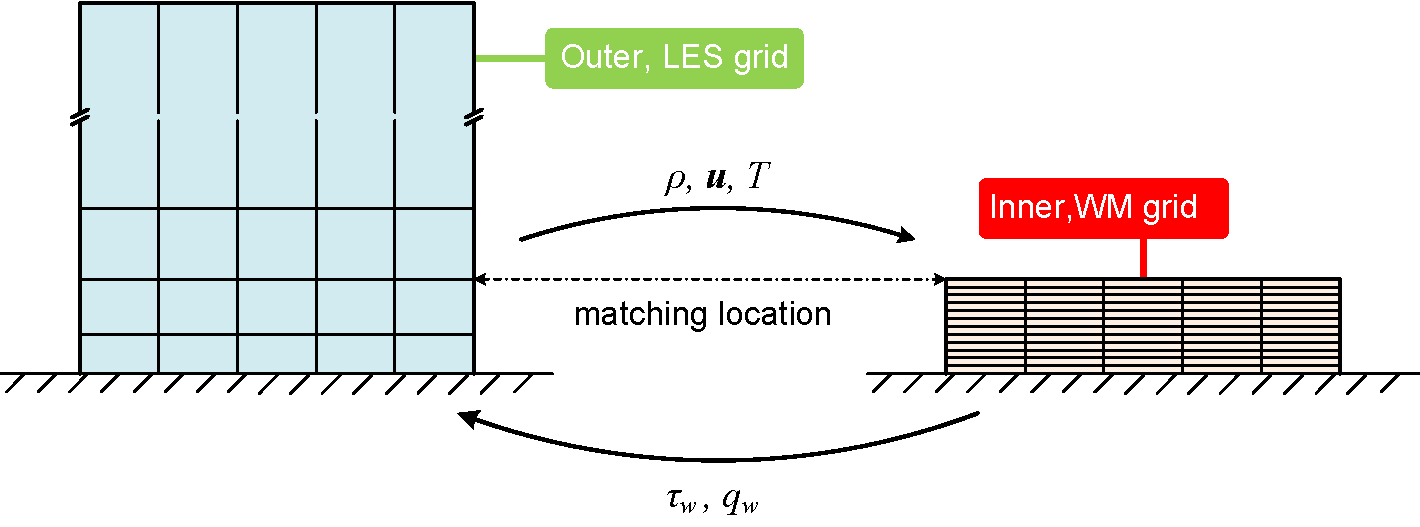
Once the wall model equations are solved, the wall shear stress $\tau_w$ and wall heat flux $q_w$ (for isothermal wall) can be computed and added back to the LES equations to compensate the effects of under-resolved boundary layer.

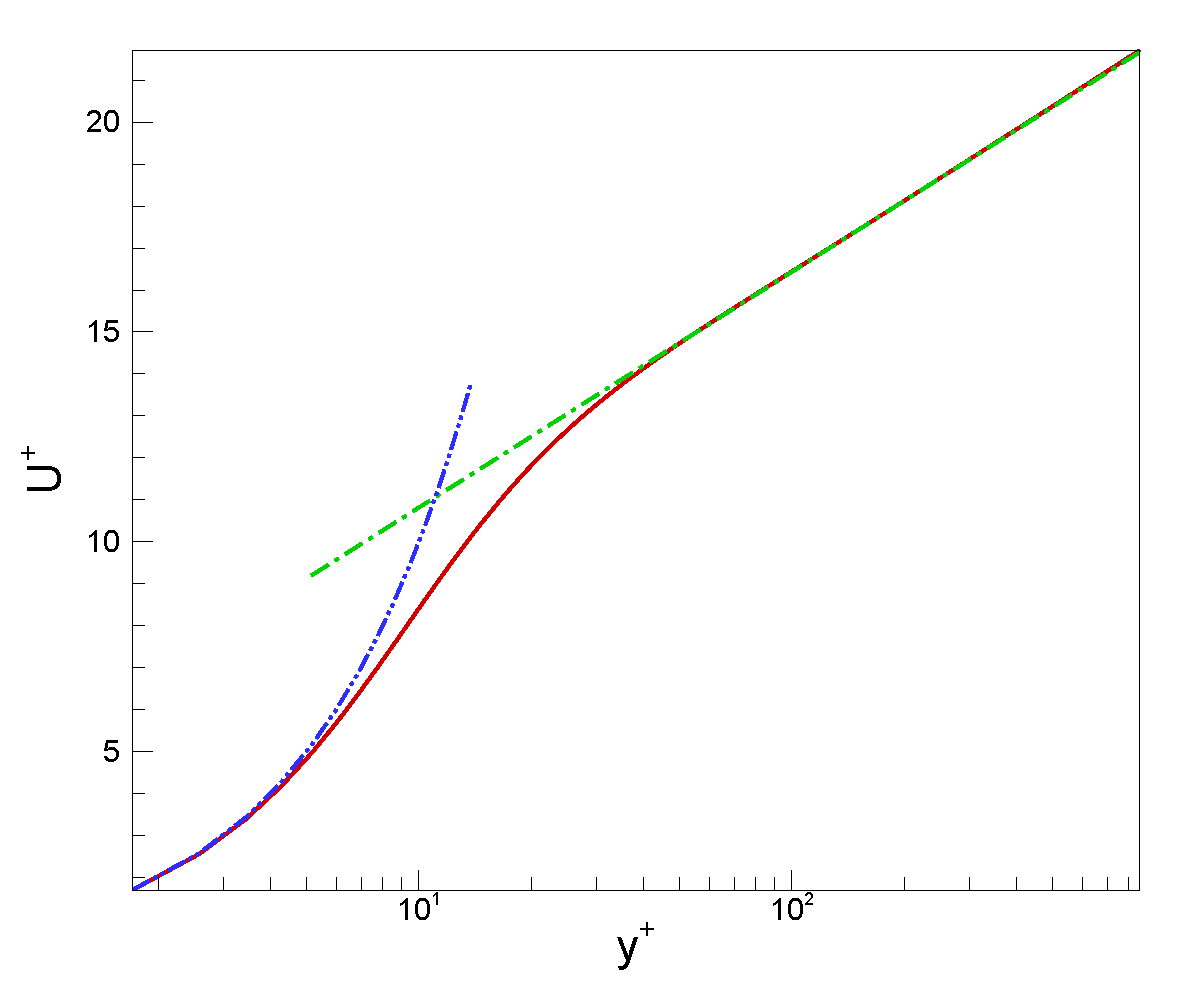
The wall model equations must at least be able to predict the correct turbulent boundary layer velocity profile. To validate this, we solve them outside the flow solver. The top boundary condition is taken from the mean flow field of a flat plate turbulent boundary layer at $Re_\theta=2800$. The wall model grid is much refined with a grid spacing of $\Delta y^+=0.5$. The figure below compares the velocity profiles from the wall model equations (red solid line) and the linear relation ($U^+= y^+$, dashed blue line) as well as the log-law relation ($U^+=2.44 \ln y^+ + 5.2$, dashed green line), and excellent agreement is observed.